회계는 물론, 재무 분야와 주식투자 등등 각종 분야에서의 기본이 되는 화폐의 현재가치와 미래가치에 대해서 알아보는 시간을 가져보겠습니다. 어떤 상황에서도 현재가치와 미래가치를 구할 수 있도록 합시다.
화폐의 시간가치
화폐의 시간가치란 무엇일까요? 지금 현재 기준의 1억원과 5년 전 기준의 1억원이 같은 가치일까요?
또는, 지금 현재 기준의 1억원과 5년 후 기준의 1억원은 같은 가치일까요?
아닙니다. 현재 1억원은 과거와 미래가 모두 그 가치가 다릅니다.
27년 전 제가 어렸을때는 오징어땅콩 한 봉지가 500원이었습니다. 하지만 지금은 무려 3,000원이나 합니다. 이렇게 돈의 가치는 시간이 지날수록 변하게 됩니다.
이러한 현상을 두고 “화폐의 시간가치”가 변한다고 할 수 있습니다.
회계에서의 현재가치
회계에서 통상 이야기하는현재가치를 산출하기 위해서는 “미래의 현금흐름”과 “시장이자율=유효이자율”이 존재해야 합니다. 즉 현재가치는 “미래의 현금흐름”을 “시장이자율 또는 유효이자율”로 할인한 개념이라고 할 수 있습니다.
시장이자율(=유효이자율)이란 현재 내가 가진 돈을 누군가에게 빌려주거나 투자했을 때 받을 수 있는 “이자율의 시세”라고 생각하시면 됩니다. 쉽게 말하면, “내가 이 돈을 어딘가 투자하면 이정도 이자율은 받는다”는 개념입니다.
그렇다면, 아래 2가지 사례로 현재가치를 공부해보겠습니다.
ㄱ. 현재는 2021년 1월 1일이며, 3년 후인 2023년 12월 31일 1,000,000원을 수령하고, 매년 말 50,000원씩 배당금을 수령 할 수 있는 상품이 있습니다. 현재 연간 시장이자율(유효이자율)은 10%입니다. 이 상품의 현금흐름과 현재가치를 분석해 보겠습니다.
사례에서 3년후 만기에 받을 1,000,000원을 “액면금액 또는 액면가액”이라고 합니다. 50,000원을 “액면이자 또는 표시이자”라고 하며, 50,000원의 표시이자는 액면금액 1,000,000원 대비 5%에 해당되어 이 5%를 “액면이자율 또는 표시이자율”이라고 합니다.
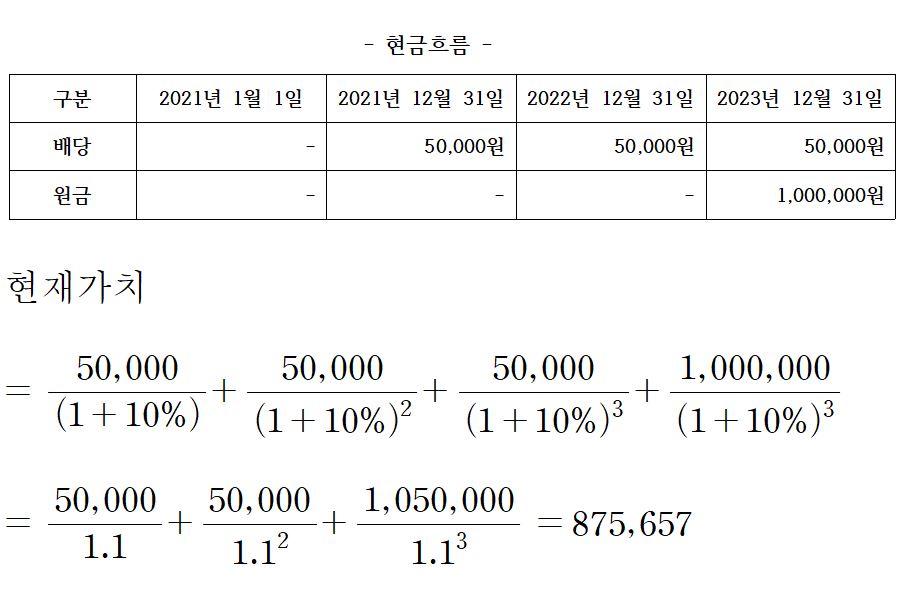
위의 사진과 같이, 사례 상품의 현재가치는 875,657원으로 산출이 되는 것을 알 수 있습니다.
즉, 위 상품은 2021년 1월 1일 현재 875,657원을 주면 3년간 매년말 50,000원의 이자와 만기인 2023년 12월 31일 1,000,000원의 원금(액면금액 또는 액면가액)을 받을 수 있는 것입니다. 이 말을 달리 해석하면, 위 사례 조건의 상품은 2021년 1월 1일 현재 시장에서 875,657원에 거래된다는 말이기도 합니다. 이를 “공정가치”라고 합니다.
다음 사례를 살펴보겠습니다.
ㄴ. 현재는 2021년 1월 1일이며, 1년 6개월 후인 2022년 6월 30일 1,000,000원을 수령하고, 6개월마다 20,000원씩 총 3번 배당금을 수령 할 수 있는 상품이 있습니다. 현재 연간 시장이자율(유효이자율)은 8%입니다. 이 상품의 현금흐름과 현재가치를 분석해 보겠습니다.
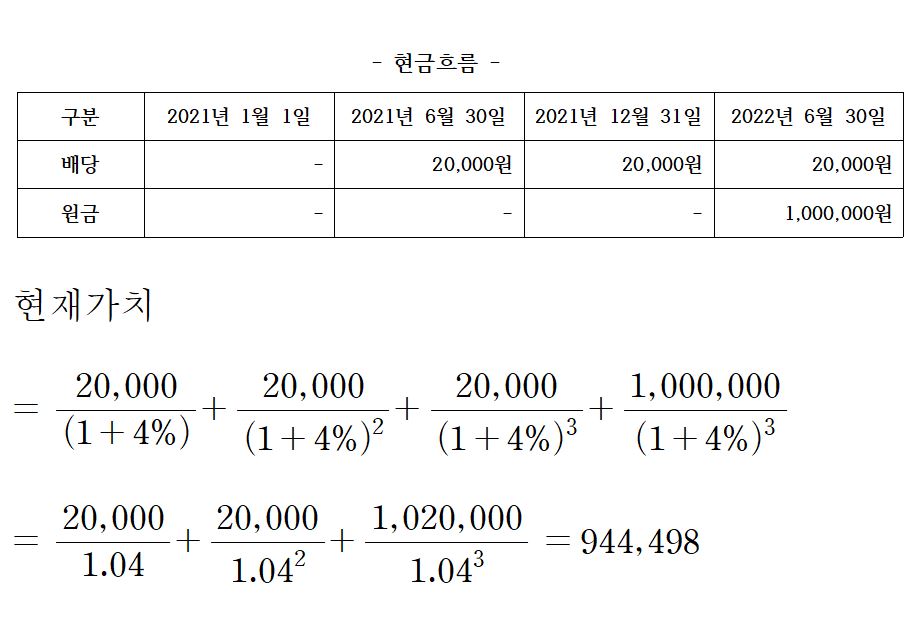
위의 사진과 같이, 사례 상품의 현재가치는 944,498원으로 산출이 되는 것을 알 수 있습니다.
즉, 위 상품은 2021년 1월 1일 현재 944,498원을 주면 1년 6개월간 매 6개월 마다 20,000원의 이자와 만기인 2022년 6월 30일 1,000,000원의 원금(액면금액 또는 액면가액)을 받을 수 있는 것입니다. 이 말을 달리 해석하면, 위 사례 조건의 상품은 2021년 1월 1일 현재 시장에서 944,498원에 거래된다는 말이기도 합니다. 이를 “공정가치”라고 합니다.
그런데, 여러분! 굉장히 특이하죠? 6개월 마다 이자를 계산합니다!
연간 시장이자율이 8%라고 하였으나 6개월간의 시장이자율로 환산해서 4%를 적용해야 되는 것입니다. 헷갈릴 수 있지만, 분모에 들어간 제곱과 세제곱이 나타내는 의미를 정확히 파악해야 합니다. 제곱은 기간이 2개의 기간이라는 의미이고, 세제곱은 3개의 기간이라는 것입니다. 즉 1개의 기간이 6개월이며 두 번째 이자를 수령하는 2021년 12월 31일에서부터 현재 시점인 2021년 1월 1일까지는 2개의 기간이기 때문에, 분모에 4%에 해당하는 1기간의 이자율을 2개의 기간으로 현재가치화하여 제곱 산식을 쓴 것입니다. 1년만이 1기간이라고 생각하시면 절대 안됩니다. 결국, 현재가치 계산시 분모에 들어가는 제곱이나 세제곱의 경우 모두 “기간”이 몇 개의 기간인가를 따져야 되는 것입니다.
회계에서의 미래가치
미래가치는 현재가치의 정확히 반대 개념입니다. 현재가치는 나누는 개념이었다면, 미래가치는 미래를 향해 곱해가는 개념입니다. 사례를 통해 미래가치를 살펴보겠습니다.
현재는 2021년 1월 1일이며 1,000,000원짜리 물건이 있다고 가정합니다. 이 물건은 현 시점부터 매 3개월마다 70,000원씩 고정 수익을 창출해 주며, 2021년 12월 31일까지 수익이 창출된다고 가정합니다. 또한, 연간 시장이자율은 12%라고 가정합시다.
이 자산의 현금흐름과 2021년 12월 31일 기준 미래가치를 아래와 같이 살펴봅시다.
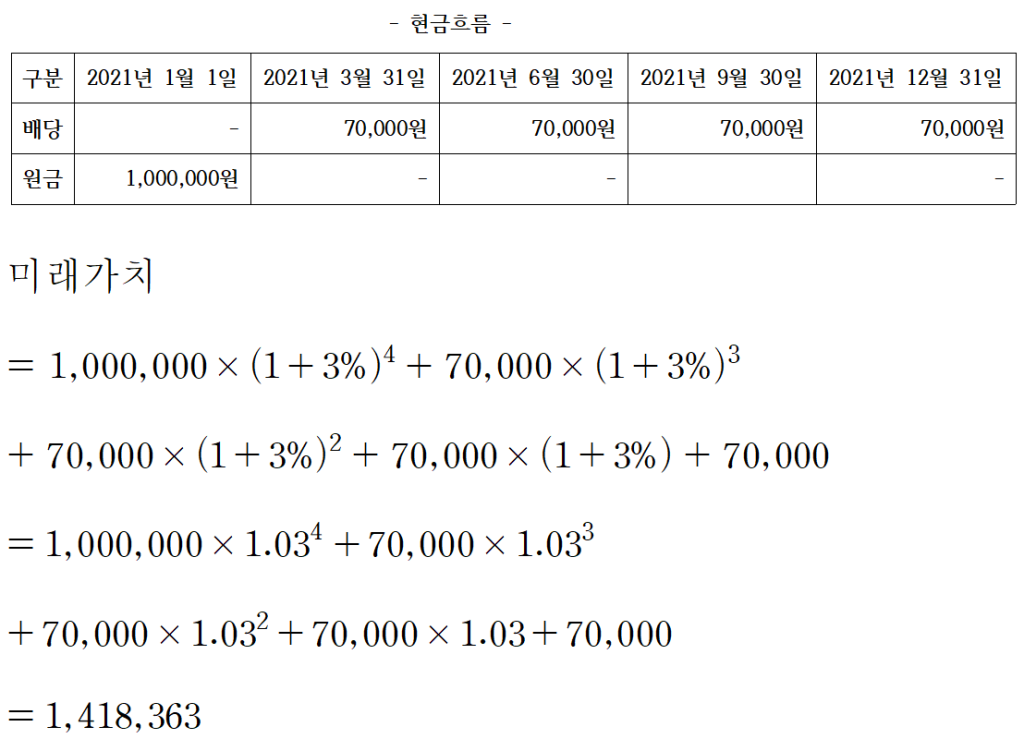
역시 위 사례도 1기간을 가지고 생각해봐야 합니다. 1기간이 3개월이며, 1기간(3개월)의 시장이자율은 12%가 아닌 3개월 치 이자율인 3%입니다. 따라서 4기간이 종료되는 1년후인 2021년 12월 31일 기준의 미래가치는 위의 산식과 같이 계산되는 것입니다.
오늘은 회계에서 말하는 현재가치와 미래가치에 대해서 자세히 알아보았습니다.